Hello,
I want to ask if anyone knows how to implement in oemof.solph the following problem:
I have Energysystem which inculdes a storage.
I have limeted the maximum input and outpu flow of the storage.
Now i realised that the maximum input and output flow depends on the state of charge of the storage.
E.g.: Wenn the storage is empty I can load it with the full maximum input flow. But when the storage is full at 90% I am only able to load it with 0.2*maximum input flow.
Does any one know if this is possible to implement in oemof and if yes how?
THX for any help
Yours Thomas
Hi @TomK,
Doing this will need you to either change the class GenericStorage or to manually add a constraint after the model is build. If the relation between SOC and the flow limit is linear the second option is most probably the easier one. The constraint could look like oemof.solph.constraints.equate_variables (documentation of oemof.solph 0.5.0 at oemof-solph.readthedocs.io) but using “<=” instead of “==”. So, the question is whether something in the style of “Flow[grid, battery] <= (1 - SOC) * P_max” is good enough to describe your problem. If not, additional (integer) variables are needed.
Cheers,
Patrik
Hi @pschoen ,
THX for the information!
I will try it.
Do you know if it is possible to use a “if” in the constraints?
So I can say between a SOC of 0% and 80% this linear function should be used and between a SOC of 80% and 100% the other linear function should be used.
Yours
Thomas
Hi @TomK,
The description is purely based on declarative relations (such as equations), so unfortunately, no “if” is possible. However, there is a solution that uses a binary variable. End of last year, I commented on it in arXiv:2211.14080. Equations 3 formulates the “if” condition and Eq. 4 reformulates it using binary variables.
Cheers,
Patrik
Hi @pschoen,
Hmmm…
I try to clearfy my problem a little better.
I have at the moment my storage as followed:
el_storage = solph.components.GenericStorage(
nominal_storage_capacity=3000,
label="electrical_storage",
inputs={bus_el: solph.Flow(nominal_value=2400)},
outputs={bus_el: solph.Flow(nominal_value=2400)},
loss_rate=0.0,
initial_storage_level=0.5,
inflow_conversion_factor=0.965,
outflow_conversion_factor=0.965,
)
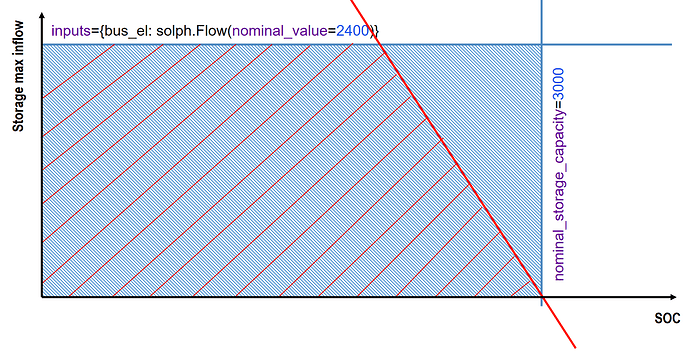
So when i interpert this in the right way i will get as solution space for the allowed input flow the blue area in the image.
Now i want to inculde the linear function which represents the red line. So i want to limit the solution space to the red area.
So can i do this in they way you showed before with the constraints.equate_variables?
Yours
Thomas
Thank you for the visual representation. I got your problem before but having it graphic helped me to find another way that works without “if” (or binary variables). You can add a constraint that limits charging to 5 * nominal_value * (1 - soc) in the same way constraints.equate_variables is implemented. Below a SOC of 80 %, it will not have any effect as the regular limit is lower. Above, it will automatically be the only relevant constraint.
import pandas as pd
import numpy as np
import logging
import os
import pprint as pp
import matplotlib.pyplot as plt
from pyomo.environ import Constraint
from oemof import solph
from pyomo import environ as po
def equate_variables(model, var1, var2, var3, factor1=1, name=None):
if name is None:
name = "_".join(["equate", str(var1), str(var2),str(var3)])
def equate_variables_rule(m):
return var3 <= 5*var2*(1-var1)
setattr(model, name, po.Constraint(rule=equate_variables_rule))
def run_oemof():
my_index = pd.date_range(start='04/08/2019', periods=672, freq='15min')
my_energysystem = solph.EnergySystem(timeindex=my_index, infer_last_interval=True)
# csv Datei einlesen
csvFile = pd.read_csv(r"..\Data\Input_Data_Dymola\Input_Dataframe_FMU.txt",
sep=";", decimal=".", thousands=",", header=None)
# Definition der Buse des Energiesystems und hinzufügen zum Energiesystem
bus_el = solph.Bus(label="electricity")
bus_gas = solph.Bus(label="gas")
bus_heat = solph.Bus(label="heat")
bus_cool = solph.Bus(label="cool")
my_energysystem.add(bus_el)
my_energysystem.add(bus_gas)
my_energysystem.add(bus_heat)
my_energysystem.add(bus_cool)
# Definition der Sources
my_energysystem.add(solph.components.Source(label='el_Netz', outputs={bus_el: solph.Flow(
variable_costs=csvFile[13]+0.04406,investment=solph.Investment(ep_costs=51.998))}))
my_energysystem.add(solph.components.Source(label='el_PV', outputs={bus_el: solph.Flow(
fix=csvFile[4], nominal_value=4)}))
my_energysystem.add(solph.components.Source(label='gas_Netz', outputs={bus_gas: solph.Flow(
variable_costs=0.027)}))
# Definition der Sinks
my_energysystem.add(solph.components.Sink(label='electricity_demand', inputs={bus_el: solph.Flow(
fix=csvFile[1], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='heat_demand', inputs={bus_heat: solph.Flow(
fix=csvFile[2], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='cool_demand', inputs={bus_cool: solph.Flow(
fix=csvFile[3], nominal_value=4)}))
# create excess components to allow overproduction
my_energysystem.add(solph.components.Sink(label="excess_bus_el", inputs={bus_el: solph.Flow()}))
my_energysystem.add(solph.components.Sink(label="excess_bus_heat", inputs={bus_heat: solph.Flow()}))
# Definition der Transformers
my_energysystem.add(solph.components.Transformer(
label="Chiller",
inputs={bus_el: solph.Flow()},
outputs={bus_cool: solph.Flow(nominal_value=4000),
bus_heat: solph.Flow(nominal_value=4000)},
conversion_factors={bus_cool: 2.8, bus_heat: 2.85}))
my_energysystem.add(solph.components.Transformer(
label="gas_boiler",
inputs={bus_gas: solph.Flow()},
outputs={bus_heat: solph.Flow(nominal_value=10e10)},
conversion_factors={bus_heat: 0.9}))
my_energysystem.add(solph.components.Transformer(
label="heat_pump",
inputs={bus_el: solph.Flow(nominal_value=40)},
outputs={bus_heat: solph.Flow()},
conversion_factors={bus_heat: 4.971538}))
# Definition der Storages and add them to esys
el_storage = solph.components.GenericStorage(
nominal_storage_capacity=3000,
label="electrical_storage",
inputs={bus_el: solph.Flow(nominal_value=2400)},
outputs={bus_el: solph.Flow(nominal_value=2400)},
loss_rate=0.0,
initial_storage_level=0.5,
inflow_conversion_factor=0.965,
outflow_conversion_factor=0.965,
)
heat_storage = solph.components.GenericStorage(
nominal_storage_capacity=4000,
label="heat_storage",
inputs={bus_heat: solph.Flow(nominal_value=1396.67)},
outputs={bus_heat: solph.Flow(nominal_value=1396.67)},
loss_rate=0.0001,
initial_storage_level=0.5,
inflow_conversion_factor=0.99999,
outflow_conversion_factor=0.99999,
)
my_energysystem.add(el_storage)
my_energysystem.add(heat_storage)
om = solph.Model(my_energysystem)
#------------Adaption------------------------------------------
soc = 1010 # state of charge
nominal_value = 2400
flow = 1010 # electrical_storage input flow from el_bus
solph.constraints.equate_variables(
om,
soc,
nominal_value,
flow)
#---------------------------------------------------------------
om.solve(solver='gurobi', solve_kwargs={'tee': True})
# Ausgabe für Berechnung
results = solph.processing.results(om)
oemof_result=pd.DataFrame()
for ob in results.keys():
new_df = results[ob]['sequences']
label = 'VON: ' + ob[0].label+' [kWh]'
faktor=1
if hasattr(ob[1], 'label'):
label = 'VON: ' + ob[0].label + ' ' + 'ZU: ' + ob[1].label+' [kWh]'
faktor=4
new_df = new_df.rename(columns={new_df.columns[0]: label})/faktor
oemof_result = pd.concat([oemof_result, new_df], axis=1)
return oemof_result, my_energysystem
result_tuple=run_oemof()
Hi @pschoen ,
sorry for the late answer.
I tried now to implement in my code what we have discussed before.
I copied the code into here as you can see above.
I am stil struggeling with some points:
-
I don’t know how to adrers the state of charge. It is changed during the optimisation and I don’t know how to get it before the optimisation starts.
-
I am also not shure how to select the input flow from the electrical storage.
-
I hope the formular is working in that way
Do you have any suggestions how to solve it?
The changed parts are in “adaption” and the “def equate_variables”.
THX
Thomas
Hi @TomK,
The additional constraints can be added after the model is created. You already did that. The variable for the storage content actually has two dimensions, one index is for the storage component (the GenericStorage object), one is for the time step t in m.TIMESTEPS. The equation in the constraint should look something like this in your case:
1/ full_charging_limit * nominal_value * (
1 - m.GenericStorageBlock.storage_content[storage_component, t + 1] / storage_capacity
) >= m.flow[i, o, t]
The parameter full_charging_limit gives the share that cannot be charged at the full rate. Note that I put “+ 1” to the time, so that charging slows down if the limit is passed within the time step.
Cheers,
Patrik
Hi @pschoen,
I tried to insert your formular. I got the following Error:
ERROR: Rule failed when generating expression for Constraint equate with index
0: TypeError: equate_variables2..equate_variables_rule() missing 1
required positional argument: ‘t’
I am still not shure how the program knows that model.flow[i,o,t] is the input flow from the electrical storage. Because “model” includes the whole energy model. As “storage_component” I insert the name of the electrical storage. Here I am not shure if I have to use “el_storage” or the lable “electrical_storage”.
THX
Thomas
Here is the updated code:
import pandas as pd
import numpy as np
import logging
import os
import pprint as pp
import matplotlib.pyplot as plt
from pyomo.environ import Constraint
from oemof import solph
from pyomo import environ as po
def equate_variables2(model, name=None):
if name is None:
name = "_".join(["equate"])
full_charging_limit = 0.8
nominal_value = 2400
storage_capacity = 3000
def equate_variables_rule(i,o,t):
return 1/ full_charging_limit * nominal_value * (1 - model.GenericStorageBlock.storage_content["el_storage", t + 1] / storage_capacity) >= model.flow[i, o, t]
setattr(model, name, po.Constraint(model.TIMESTEPS, rule=equate_variables_rule))
def run_oemof():
my_index = pd.date_range(start='04/08/2019', periods=672, freq='15min')
my_energysystem = solph.EnergySystem(timeindex=my_index, infer_last_interval=True)
# csv Datei einlesen
csvFile = pd.read_csv(r"..\Data\Input_Data_Dymola\Input_Dataframe_FMU.txt",
sep=";", decimal=".", thousands=",", header=None)
# Definition der Buse des Energiesystems und hinzufügen zum Energiesystem
bus_el = solph.Bus(label="electricity")
bus_gas = solph.Bus(label="gas")
bus_heat = solph.Bus(label="heat")
bus_cool = solph.Bus(label="cool")
my_energysystem.add(bus_el)
my_energysystem.add(bus_gas)
my_energysystem.add(bus_heat)
my_energysystem.add(bus_cool)
# Definition der Sources
my_energysystem.add(solph.components.Source(label='el_Netz', outputs={bus_el: solph.Flow(
variable_costs=csvFile[13]+0.04406,investment=solph.Investment(ep_costs=51.998))}))
my_energysystem.add(solph.components.Source(label='el_PV', outputs={bus_el: solph.Flow(
fix=csvFile[4], nominal_value=4)}))
my_energysystem.add(solph.components.Source(label='gas_Netz', outputs={bus_gas: solph.Flow(
variable_costs=0.027)}))
# Definition der Sinks
my_energysystem.add(solph.components.Sink(label='electricity_demand', inputs={bus_el: solph.Flow(
fix=csvFile[1], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='heat_demand', inputs={bus_heat: solph.Flow(
fix=csvFile[2], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='cool_demand', inputs={bus_cool: solph.Flow(
fix=csvFile[3], nominal_value=4)}))
# create excess components to allow overproduction
my_energysystem.add(solph.components.Sink(label="excess_bus_el", inputs={bus_el: solph.Flow()}))
my_energysystem.add(solph.components.Sink(label="excess_bus_heat", inputs={bus_heat: solph.Flow()}))
# Definition der Transformers
my_energysystem.add(solph.components.Transformer(
label="Chiller",
inputs={bus_el: solph.Flow()},
outputs={bus_cool: solph.Flow(nominal_value=4000),
bus_heat: solph.Flow(nominal_value=4000)},
conversion_factors={bus_cool: 2.8, bus_heat: 2.85}))
my_energysystem.add(solph.components.Transformer(
label="gas_boiler",
inputs={bus_gas: solph.Flow()},
outputs={bus_heat: solph.Flow(nominal_value=10e10)},
conversion_factors={bus_heat: 0.9}))
my_energysystem.add(solph.components.Transformer(
label="heat_pump",
inputs={bus_el: solph.Flow(nominal_value=40)},
outputs={bus_heat: solph.Flow()},
conversion_factors={bus_heat: 4.971538}))
# Definition der Storages and add them to esys
el_storage = solph.components.GenericStorage(
nominal_storage_capacity=3000,
label="electrical_storage",
inputs={bus_el: solph.Flow(nominal_value=2400)},
outputs={bus_el: solph.Flow(nominal_value=2400)},
loss_rate=0.0,
initial_storage_level=0.5,
inflow_conversion_factor=0.965,
outflow_conversion_factor=0.965,
)
heat_storage = solph.components.GenericStorage(
nominal_storage_capacity=4000,
label="heat_storage",
inputs={bus_heat: solph.Flow(nominal_value=1396.67)},
outputs={bus_heat: solph.Flow(nominal_value=1396.67)},
loss_rate=0.0001,
initial_storage_level=0.5,
inflow_conversion_factor=0.99999,
outflow_conversion_factor=0.99999,
)
my_energysystem.add(el_storage)
my_energysystem.add(heat_storage)
om = solph.Model(my_energysystem)
#------------Adaption------------------------------------------
equate_variables2(
om)
#---------------------------------------------------------------
om.solve(solver='gurobi', solve_kwargs={'tee': True})
# Ausgabe für Berechnung
results = solph.processing.results(om)
oemof_result=pd.DataFrame()
for ob in results.keys():
new_df = results[ob]['sequences']
label = 'VON: ' + ob[0].label+' [kWh]'
faktor=1
if hasattr(ob[1], 'label'):
label = 'VON: ' + ob[0].label + ' ' + 'ZU: ' + ob[1].label+' [kWh]'
faktor=4
new_df = new_df.rename(columns={new_df.columns[0]: label})/faktor
oemof_result = pd.concat([oemof_result, new_df], axis=1)
return oemof_result, my_energysystem
result_tuple=run_oemof()
I was a bit sloppy here, in particular because I also don’t always do everything correct instantly and often have to try myself.
m.flow[i, o, t] was the standard formulation, denoting the flow from i to o at point t. In your case, it would translate to:
def equate_variables_rule(t):
return 1/ full_charging_limit * nominal_value * (1 - model.GenericStorageBlock.storage_content[el_storage, t + 1] / storage_capacity) >= model.flow[bus_el, el_storage, t]
For the index, it should be the instance of the object and not the string representation of the label. (Both might work, but the string is definitely not the commonly used option.)
Doesn’t matter. I am happy that someone can help me.
I tried it know in this way:
return 1 / full_charging_limit * nominal_value * (
1 - model.GenericStorageBlock.storage_content['el_storage', t + 1] / storage_capacity) >= \
model.flow['bus_el', 'el_storage', t]
But I get the error message:
File "C:/Users/TKurz/Documents/DISS/GitHub/Dymola_Neural_Network/Scripts/oemof_model.py", line 31, in equate_variables_rule
1 - model.GenericStorageBlock.storage_content['el_storage', t + 1] / storage_capacity) >= \
TypeError: unsupported operand type(s) for +: 'Model' and 'int'
Therefore i also tried this:
return 1 / full_charging_limit * nominal_value * (
1 - model.GenericStorageBlock.storage_content['electrical_storage', t + 1] / storage_capacity) >= \
model.flow['electricity', 'electrical_storage', t]
But I got the same error message.
I also tryed to insert instead of ‘el_storage’ something like model.el_storage or model.xxx.storage but I was only able to receive the error that this component dosen’t exist.
Sorry that I have so many questions ![]()
THX
Thomas
For some reason, t seems to be your model. I think, your code should contain something like the following:
my_energysystem.add(el_storage, bus_el)
model = solph.Model(my_energysystem)
def soc_limit_rule(t):
return (
1/ full_charging_limit * nominal_value * (
1 - model.GenericStorageBlock.storage_content[el_storage, t + 1]
/ storage_capacity)
>= model.flow[bus_el, el_storage, t]
)
setattr(
model,
"soc_limit",
po.Constraint(
model.TIMESTEPS,
noruleinit=True,
),
)
setattr(
model,
"soc_limit_build",
po.BuildAction(rule=soc_limit_rule),
)
(Did not test it, but maybe it helps you.)
PS: I just added a pretty similar constraint to solph, that allows for stepwise limits: Add storage_level_constraint by p-snft · Pull Request #936 · oemof/oemof-solph (github.com). Maybe, also that one can serve as a basis for your own constraint.
Hi,
I tried it with your suggestions, but I wasn’t able to run it.
A friend of mine has built an extra class for the storage and with this it worked.
The new customised storage class:
from oemof.network import network as on
from pyomo.core.base.block import ScalarBlock
from pyomo.environ import BuildAction
from pyomo.environ import Constraint
from pyomo.environ import Piecewise
from pyomo.environ import NonNegativeReals
from pyomo.environ import Set
from pyomo.environ import Var
from oemof.solph._plumbing import sequence as solph_sequence
from oemof.solph._options import Investment
from oemof.solph._helpers import check_node_object_for_missing_attribute
from oemof import network as solph_network
class CustomStorage(on.Node):
def __init__(
self, *args, max_storage_level=1, min_storage_level=0, **kwargs
):
super().__init__(*args, **kwargs)
self.nominal_storage_capacity = kwargs.get("nominal_storage_capacity")
self.initial_storage_level = kwargs.get("initial_storage_level")
self.balanced = kwargs.get("balanced", True)
self.breakpoints = list(kwargs.get("breakpoints"))
self.y_points_storage_in = kwargs.get("y_points_storage_in")
self.y_points_storage_out = kwargs.get("y_points_storage_out")
self.pw_repn = kwargs.get("pw_repn")
self.loss_rate = solph_sequence(kwargs.get("loss_rate", 0))
self.fixed_losses_relative = solph_sequence(kwargs.get("fixed_losses_relative", 0))
self.fixed_losses_absolute = solph_sequence(kwargs.get("fixed_losses_absolute", 0))
self.inflow_conversion_factor = solph_sequence(kwargs.get("inflow_conversion_factor", 1))
self.outflow_conversion_factor = solph_sequence(kwargs.get("outflow_conversion_factor", 1))
self.max_storage_level = solph_sequence(max_storage_level)
self.min_storage_level = solph_sequence(min_storage_level)
self.investment = kwargs.get("investment")
self.invest_relation_input_output = kwargs.get("invest_relation_input_output")
self.invest_relation_input_capacity = kwargs.get("invest_relation_input_capacity")
self.invest_relation_output_capacity = kwargs.get("invest_relation_output_capacity")
self._invest_group = isinstance(self.investment, Investment)
# Check number of flows.
self._check_number_of_flows()
# Check attributes for the investment mode.
if self._invest_group is True:
self._check_invest_attributes()
def _set_flows(self):
for flow in self.inputs.values():
if (
self.invest_relation_input_capacity is not None
and not isinstance(flow.investment, Investment)
):
flow.investment = Investment()
for flow in self.outputs.values():
if (
self.invest_relation_output_capacity is not None
and not isinstance(flow.investment, Investment)
):
flow.investment = Investment()
def _check_invest_attributes(self):
if self.investment and self.nominal_storage_capacity is not None:
e1 = (
"If an investment object is defined the invest variable "
"replaces the nominal_storage_capacity.\n Therefore the "
"nominal_storage_capacity should be 'None'.\n"
)
raise AttributeError(e1)
if (
self.invest_relation_input_output is not None
and self.invest_relation_output_capacity is not None
and self.invest_relation_input_capacity is not None
):
e2 = (
"Overdetermined. Three investment object will be coupled"
"with three constraints. Set one invest relation to 'None'."
)
raise AttributeError(e2)
if (
self.investment
and sum(solph_sequence(self.fixed_losses_absolute)) != 0
and self.investment.existing == 0
and self.investment.minimum == 0
):
e3 = (
"With fixed_losses_absolute > 0, either investment.existing "
"or investment.minimum has to be non-zero."
)
raise AttributeError(e3)
self._set_flows()
def _check_number_of_flows(self):
msg = "Only one {0} flow allowed in the GenericStorage {1}."
check_node_object_for_missing_attribute(self, "inputs")
check_node_object_for_missing_attribute(self, "outputs")
if len(self.inputs) > 1:
raise AttributeError(msg.format("input", self.label))
if len(self.outputs) > 1:
raise AttributeError(msg.format("output", self.label))
def constraint_group(self):
return CustomStorageBlock
class CustomStorageBlock(ScalarBlock):
CONSTRAINT_GROUP = True
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
def _create(self, group=None):
m = self.parent_block()
if group is None:
return None
i = {n: [i for i in n.inputs][0] for n in group}
o = {n: [o for o in n.outputs][0] for n in group}
self.CUSTOMSTORAGES = Set(initialize=[n for n in group])
self.STORAGES_BALANCED = Set(initialize=[n for n in group if n.balanced is True])
self.STORAGES_WITH_INVEST_FLOW_REL = Set(
initialize=[n for n in group if n.invest_relation_input_output is not None])
pw_repns = [n.pw_repn for n in group]
if all(x == pw_repns[0] for x in pw_repns):
self.pw_repn = pw_repns[0]
self.breakpoints = {}
self.y_points_storage_in = {}
self.y_points_storage_out = {}
def build_breakpoints(block, n):
for t in m.TIMESTEPS:
self.breakpoints[(n, t)] = n.breakpoints
self.y_points_storage_in[(n, t)] = n.y_points_storage_in
self.y_points_storage_out[(n, t)] = n.y_points_storage_out
self.breakpoint_build = BuildAction(self.CUSTOMSTORAGES, rule=build_breakpoints)
def _storage_content_bound_rule(block, n, t):
bounds = (n.nominal_storage_capacity * n.min_storage_level[t],
n.nominal_storage_capacity * n.max_storage_level[t])
return bounds
self.storage_content = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=_storage_content_bound_rule)
self.Outflow_Bound = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(0, 100000))
self.Inflow_Bound = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(0, 100000))
self.Outflow_Var = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(-100000, 0))
self.Inflow_Var = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(-100000, 0))
self.Outflow = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(0, 100000))
self.Inflow = Var(self.CUSTOMSTORAGES, m.TIMESTEPS, bounds=(0, 100000))
self.piecewise_out = Piecewise(
self.CUSTOMSTORAGES,
m.TIMESTEPS,
self.Outflow_Bound,
self.storage_content,
pw_repn=self.pw_repn,
#force_pw=True,
pw_constr_type="EQ",
pw_pts=self.breakpoints,
f_rule=self.y_points_storage_out,
)
self.piecewise_in = Piecewise(
self.CUSTOMSTORAGES,
m.TIMESTEPS,
self.Inflow_Bound,
self.storage_content,
pw_repn=self.pw_repn,
#force_pw=True,
pw_constr_type="EQ",
pw_pts=self.breakpoints,
f_rule=self.y_points_storage_in,
)
def Outflow_expression(block, n, t):
expr = 0
expr += self.Outflow_Bound[n, t]
expr += -self.Outflow[n, t]
expr += self.Outflow_Var[n, t]
return expr == 0
self.Outflow_Constraint = Constraint(self.CUSTOMSTORAGES, m.TIMESTEPS, rule=Outflow_expression)
def Inflow_expression(block, n, t):
expr = 0
expr += self.Inflow_Bound[n, t]
expr += -self.Inflow[n, t]
expr += self.Inflow_Var[n, t]
return expr == 0
self.Inflow_Constraint = Constraint(self.CUSTOMSTORAGES, m.TIMESTEPS, rule=Inflow_expression)
def _storage_init_content_bound_rule(block, n):
return 0, n.nominal_storage_capacity
self.init_content = Var(self.CUSTOMSTORAGES, within=NonNegativeReals, bounds=_storage_init_content_bound_rule)
# for n in group:
# if n.initial_storage_level is not None:
# self.init_content[n] = (n.initial_storage_level * n.nominal_storage_capacity)
# self.init_content[n].fix()
reduced_timesteps = [x for x in m.TIMESTEPS if x > 0]
def _Inflow_rule(block, n, t):
expr = 0
expr += -m.flow[list(n.inputs.keys())[0], n, t]
expr += self.Inflow[n, t]
return expr == 0
self.Inflow_rule = Constraint(self.CUSTOMSTORAGES, m.TIMESTEPS, rule=_Inflow_rule)
def _Outflow_rule(block, n, t):
expr = 0
expr += -m.flow[n, list(n.outputs.keys())[0], t]
expr += self.Outflow[n, t]
return expr == 0
self.Outflow_rule = Constraint(self.CUSTOMSTORAGES, m.TIMESTEPS, rule=_Outflow_rule)
def _storage_balance_first_rule(block, n):
expr = 0
expr += block.storage_content[n, 0]
expr += (-block.init_content[n] * (1 - n.loss_rate[0]) ** m.timeincrement[0])
expr += (n.fixed_losses_relative[0] * n.nominal_storage_capacity * m.timeincrement[0])
expr += n.fixed_losses_absolute[0] * m.timeincrement[0]
expr += (-m.flow[i[n], n, 0] * n.inflow_conversion_factor[0]) * m.timeincrement[0]
expr += (m.flow[n, o[n], 0] / n.outflow_conversion_factor[0]) * m.timeincrement[0]
return expr == 0
self.balance_first = Constraint(self.CUSTOMSTORAGES, rule=_storage_balance_first_rule)
def _storage_balance_rule(block, n, t):
expr = 0
expr += block.storage_content[n, t]
expr += (-block.storage_content[n, t - 1] * (1 - n.loss_rate[t]) ** m.timeincrement[t])
expr += (n.fixed_losses_relative[t] * n.nominal_storage_capacity * m.timeincrement[t])
expr += n.fixed_losses_absolute[t] * m.timeincrement[t]
expr += (-m.flow[i[n], n, t] * n.inflow_conversion_factor[t]) * m.timeincrement[t]
expr += (m.flow[n, o[n], t] / n.outflow_conversion_factor[t]) * m.timeincrement[t]
return expr == 0
self.balance = Constraint(self.CUSTOMSTORAGES, reduced_timesteps, rule=_storage_balance_rule)
def _balanced_storage_rule(block, n):
return (block.storage_content[n, m.TIMESTEPS[-1]] == block.init_content[n])
self.balanced_cstr = Constraint(self.STORAGES_BALANCED, rule=_balanced_storage_rule)
def _power_coupled(block, n):
expr = (m.InvestmentFlow.invest[n, o[n]] + m.flows[n, o[n]].investment.existing) * \
n.invest_relation_input_output == (
m.InvestmentFlow.invest[i[n], n] + m.flows[i[n], n].investment.existing)
return expr
self.power_coupled = Constraint(self.STORAGES_WITH_INVEST_FLOW_REL, rule=_power_coupled)
def _objective_expression(self):
if not hasattr(self, "STORAGES"):
return 0
return 0
And here my energy system:
from oemof import solph
import pandas as pd
import numpy as np
from oemof.solph.custom.heat_pump import Heatpump
from oemof.solph.custom.custom_storage import CustomStorage
#from Tools.oemof_system_plot import oemof_network_plot
#from Tools.oemof_results_plot import oemof_results_plot
my_index = pd.date_range(start='04/08/2019', periods=672, freq='15min')
my_energysystem = solph.EnergySystem(timeindex=my_index, infer_last_interval=True)
# csv Datei einlesen
csvFile = pd.read_csv(r"..\Data\Input_Data_Dymola\Input_Dataframe_FMU.txt",
sep=";", decimal=".", thousands=",", header=None)
# Definition der Buse des Energiesystems und hinzufügen zum Energiesystem
bus_el = solph.Bus(label="electricity")
bus_gas = solph.Bus(label="gas")
bus_heat = solph.Bus(label="heat")
bus_cool = solph.Bus(label="cool")
my_energysystem.add(bus_el)
my_energysystem.add(bus_gas)
my_energysystem.add(bus_heat)
my_energysystem.add(bus_cool)
# Definition der Sources
my_energysystem.add(solph.components.Source(label='el_Netz', outputs={bus_el: solph.Flow(
variable_costs=csvFile[13]+0.04406,investment=solph.Investment(ep_costs=51.998))}))
# my_energysystem.add(solph.components.Source(label='el_Netz', outputs={bus_el: solph.Flow(
# variable_costs=csvFile[13]+0.04406)}))
my_energysystem.add(solph.components.Source(label='el_PV', outputs={bus_el: solph.Flow(
fix=csvFile[4], nominal_value=4)}))
my_energysystem.add(solph.components.Source(label='gas_Netz', outputs={bus_gas: solph.Flow(
variable_costs=0.027)}))
# Definition der Sinks
my_energysystem.add(solph.components.Sink(label='electricity_demand', inputs={bus_el: solph.Flow(
fix=csvFile[1], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='heat_demand', inputs={bus_heat: solph.Flow(
fix=csvFile[2], nominal_value=4)}))
my_energysystem.add(solph.components.Sink(label='cool_demand', inputs={bus_cool: solph.Flow(
fix=csvFile[3], nominal_value=4)}))
# create excess components to allow overproduction
my_energysystem.add(solph.components.Sink(label="excess_bus_el", inputs={bus_el: solph.Flow()}))
my_energysystem.add(solph.components.Sink(label="excess_bus_heat", inputs={bus_heat: solph.Flow()}))
# Definition der Transformers
my_energysystem.add(solph.components.Transformer(
label="Chiller",
inputs={bus_el: solph.Flow()},
outputs={bus_cool: solph.Flow(nominal_value=4000),
bus_heat: solph.Flow(nominal_value=4000)},
conversion_factors={bus_cool: 2.8, bus_heat: 2.85}))
my_energysystem.add(solph.components.Transformer(
label="gas_boiler",
inputs={bus_gas: solph.Flow(nominal_value=1000000)},
outputs={bus_heat: solph.Flow(nominal_value=1000000)},
conversion_factors={bus_heat: 0.9}))
my_energysystem.add(solph.components.Transformer(
label="heat_pump",
inputs={bus_el: solph.Flow(nominal_value=40)},
outputs={bus_heat: solph.Flow()},
conversion_factors={bus_heat: 4.971538}))
#Custom storage
breakpoints = np.array([0, 600, 2400, 3000])
y_points_storage_in = np.array([2400, 2400, 2400, 1])
y_points_storage_out = np.array([1, 2400, 2400, 2400])
el_storage=CustomStorage(label='electrical_storage',
inputs={bus_el: solph.Flow(nominal_value=2400, variable_costs=0.0)},
outputs={bus_el: solph.Flow(nominal_value=2400, variable_costs=0.0)},
loss_rate=0.0,
nominal_storage_capacity=3000,
initial_storage_level=0.5,
inflow_conversion_factor=0.965,
outflow_conversion_factor=0.965,
breakpoints=breakpoints,
y_points_storage_in=y_points_storage_in,
y_points_storage_out=y_points_storage_out,
pw_repn="SOS2")
# el_storage = solph.components.GenericStorage(
# nominal_storage_capacity=3000,
# label="electrical_storage",
# inputs={bus_el: solph.Flow(nominal_value=2400)},
# outputs={bus_el: solph.Flow(nominal_value=2400)},
# loss_rate=0.0,
# initial_storage_level=0.0,
# inflow_conversion_factor=0.965,
# outflow_conversion_factor=0.965,
# )
heat_storage = solph.components.GenericStorage(
nominal_storage_capacity=4000,
label="heat_storage",
inputs={bus_heat: solph.Flow(nominal_value=1396.67)},
outputs={bus_heat: solph.Flow(nominal_value=1396.67)},
loss_rate=0.0001,
initial_storage_level=0.5,
inflow_conversion_factor=0.99999,
outflow_conversion_factor=0.99999,
)
my_energysystem.add(el_storage)
my_energysystem.add(heat_storage)
om = solph.Model(my_energysystem)
om.solve(solver='gurobi', solve_kwargs={'tee': True})
results = solph.processing.results(om)
oemof_result = pd.DataFrame()
for ob in results.keys():
new_df = results[ob]['sequences']
label = 'VON: ' + ob[0].label + ' [kWh]'
faktor = 1
if hasattr(ob[1], 'label'):
label = 'VON: ' + ob[0].label + ' ' + 'ZU: ' + ob[1].label + ' [kWh]'
faktor = 4
new_df = new_df.rename(columns={new_df.columns[0]: label}) / faktor
oemof_result = pd.concat([oemof_result, new_df], axis=1)
LG
Thomas
Thanks for sharing. I just happen to need something very similar, so I also created the constraint I was originally suggesting (to also make sure it is really possible). I am sharing this here to complement your solution.
# create an energy system
idx = pd.date_range("1/1/2023", periods=100, freq="H")
es = solph.EnergySystem(timeindex=idx,infer_last_interval=False)
# power bus
bel = solph.Bus(label="bel")
es.add(bel)
es.add(
solph.components.Source(
label="source_el",
outputs={
bel: solph.Flow(nominal_value=1, fix=1)
},
)
)
es.add(
solph.components.Sink(
label="sink_el",
inputs={
bel: solph.Flow(
nominal_value=1, variable_costs=1,
)
},
)
)
# Electric Storage
inflow_capacity = 0.5
full_charging_limit = 0.4
storage_capacity = 10
battery =solph.components.GenericStorage(
label="battery",
nominal_storage_capacity=storage_capacity,
inputs={bel: solph.Flow(nominal_value=inflow_capacity)},
outputs={bel: solph.Flow(variable_costs=2)},
initial_storage_level=0,
balanced=False,
loss_rate=0.0001,
)
es.add(battery)
# create an optimization problem and solve it
model = solph.Model(es)
def soc_limit_rule(m):
for p, ts in m.TIMEINDEX:
soc = (m.GenericStorageBlock.storage_content[battery, ts + 1]
/ storage_capacity)
expr = ((1 - soc)/(1-full_charging_limit)
>= m.flow[bel, battery, p, ts] / inflow_capacity
)
getattr(m, "soc_limit").add((p, ts), expr)
setattr(
model,
"soc_limit",
po.Constraint(
model.TIMEINDEX,
noruleinit=True,
),
)
setattr(
model,
"soc_limit_build",
po.BuildAction(rule=soc_limit_rule),
)
# solve model
model.solve(solver="cbc")
# create result object
results = solph.processing.results(model)
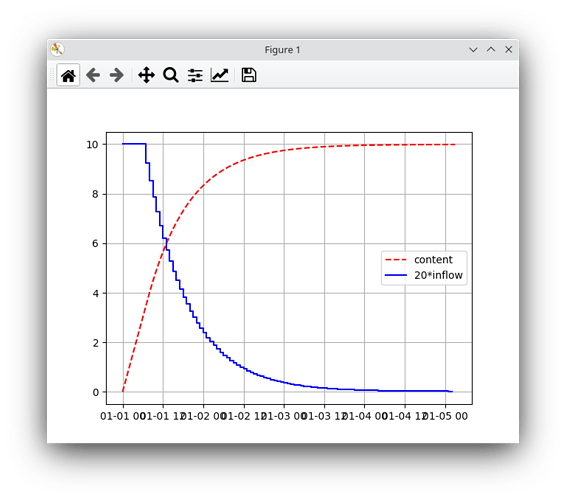
plt.plot(results[(battery, None)]["sequences"], "r--", label="content")
plt.step(10 * results[(bel, battery)]["sequences"], "b-", label="10*inflow")
plt.legend()
plt.grid()
plt.figure()
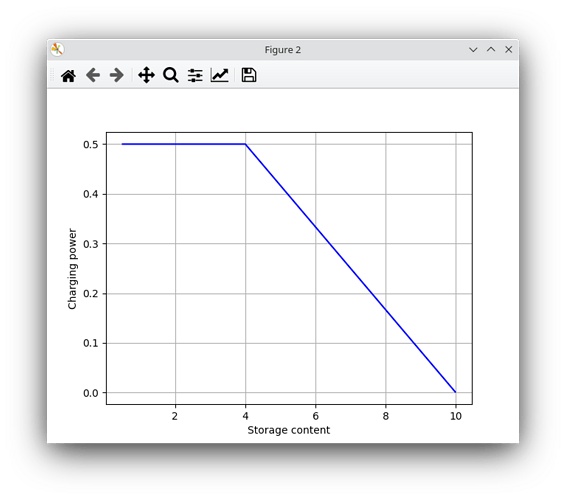
plt.plot(results[(battery, None)]["sequences"][1:], results[(bel, battery)]["sequences"][:-1])
plt.grid()
plt.xlabel("Storage content")
plt.ylabel("Charging power")
plt.show()
Storage content and inflow over time:
Storage inflow over storage content:
Maybe, it still helps.
THX @pschoen ,
looks nice!
I think it helps to understand our discussion bevore.