Hi everybody,
I’m doing my master thesis in energy system engineering and I recently discovered Oemof and Solph. I hope to use Oemof in my thesis in order to optimize a system with regard to cost. However, the main cost is due to the maximum power the system has used every month (dollars/kW and month). These kind of power tariffs are becoming more common and the most important thing is therefore to reduce the power peaks every month.
I have some real world data that I have collected for power use in a property which is added as a demand sink in my model. I also add a grid connection as a source and a battery. All three are connected to one electricity bus. The question that I struggle with is how to let Oemof know that it should optimize the use of the battery only to reduce the power peaks. As of now I have added a cost for using the battery when the demand is over some limit (currently set to the mean of the demand over the period) and zero cost when the demand is below the limit.
It works pretty good in some cases but not in others and I’m sure it can be done better. I hope some of you have some tips or suggestions! And please excuse my code, I’m very new at Python and have no real education in programming.
Is there a better way to tell Oemof how and when to use the battery? My way of setting a fixed limit seems kind of clunky. See picture below of
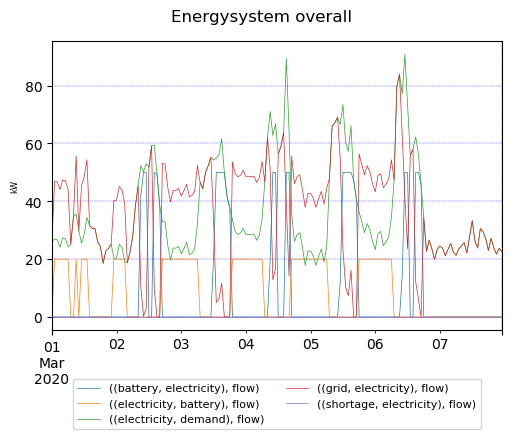
From the above picture you can see the system over 168 hours (one week). The peaks are reduced with the battery but the last peak is not reduced very efficiently.
I hope this is a reasonable question to ask and that I posted it in the right place. Thank you!
My code:
#### Load data file
filename = 'csvfile_2.csv'
data = pd.read_csv(filename)
#### Initiate model ####
solver = 'glpk' # 'glpk', 'gurobi',....
debug = False # Set number_of_timesteps to 3 to get a readable lp-file.
number_of_time_steps = 500
solver_verbose = False # show/hide solver output
date_time_index = pd.date_range('3/1/2020', periods=number_of_time_steps,
freq='H')
energysystem = solph.EnergySystem(timeindex=date_time_index)
#### Create bus for electricity flow
bel = solph.Bus(label='electricity',balanced=True)
energysystem.add(bel)
#### Sink for demand
energysystem.add(solph.Sink(label='demand', inputs={bel: solph.Flow(
nominal_value=1, actual_value=(data['demand'])/1000, fixed=True)}))
#### Grid source
energysystem.add(solph.Source(label='grid', outputs={bel: solph.Flow(nominal_value=100,
variable_costs=data['spotprice'])}))
#### Shortage output
energysystem.add(solph.Source(label='shortage', outputs={bel: solph.Flow(
variable_costs=500)}))
#### price limits for charge/discharge in order to peak shave
power_tariff_cost = 100 #SEK/kW
peak_limit = np.mean(data['demand'][0:number_of_time_steps])
Cdischarge = np.array([])
for i in range(0, len(data['demand'][0:number_of_time_steps])):
if data['demand'][i] >= peak_limit :
Cup= 0
else :
Cup= power_tariff_cost * data['demand'][i]
Cdischarge = np.append(Cdischarge, Cup)
Ccharge = np.array([])
for i in range(0, len(data['demand'][0:number_of_time_steps])):
if data['demand'][i] <= peak_limit :
Cdown= 0
else :
Cdown= power_tariff_cost * data['demand'][i]
Ccharge = np.append(Ccharge, Cdown)
#### battery model
battery_capacity = 300
battery = solph.components.GenericStorage(label='battery',
inputs={bel: solph.Flow(nominal_value=20, variable_costs=Ccharge)},
outputs={bel: solph.Flow(nominal_value=50, variable_costs=Cdischarge)},
loss_rate=0,
nominal_value=battery_capacity,
nominal_storage_capacity=battery_capacity,
inflow_conversion_factor=1,
outflow_conversion_factor=1,
balanced = True,
initial_storage_level=None,)
energysystem.add(battery)
#### Optimize system
# initialise the operational model
model = solph.Model(energysystem)
# Solve model
model.solve(solver=solver, solve_kwargs={'tee': solver_verbose})
#### Results and outputs
energysystem.results['main'] = outputlib.processing.results(model)