I am working on a UC/ED model called PowNet. Although this is not a capacity expansion model, my goal is to cut the runtime by at least half using a decomposition method (just a goal). The model has 26.8k variables and 100k constraints. The literature seems to focus on using Benders to solve stochastic capacity expansion models. In contrast, my model is simpler by not having investments and being scenario-based. I’m wondering whether anyone can give an advice or an idea on whether using a decomposition method will work (and maybe how ![]() ).
).
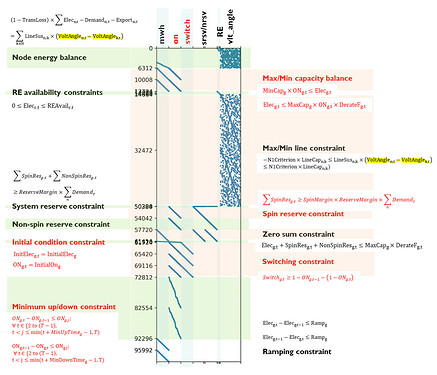
More details on this. I am looking at exploiting the structure of the problem by using the Dantzig-Wolfe decomposition. It appears that if we relax some linking constraints, then we can get a bunch of subproblems. The structure of the original problem is shown in the figure below. There are six variables as represented in the columns. The rows represent the constraints. “ON” and “SWITCH” variables are binary.
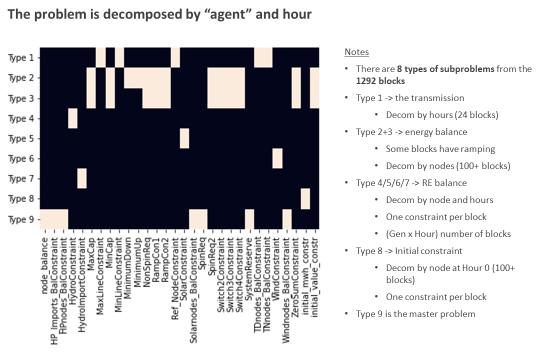
My decomposition produces 1292 subproblems and 2832 constraints in the master problem. There are eight types of subproblems. “Type 9” is the master problem.
There’s a solver that can do Dantzig-Wolfe called DSP, developed by the Argonne Lab. However, I don’t get the convergence for my problem. The work on DSP seems to have stopped since last year.
Currently I’m exploring to see whether there are other solvers so if anyone has an idea, then that would be great.
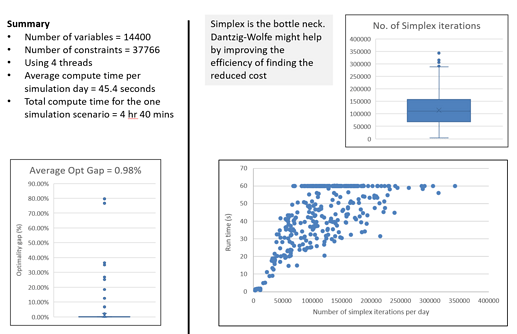
This part is just a background on why I think the DW algorithm should help. The following results are from the same PowNet model but for a different country. The grid here is smaller, and it takes on average 45 mins to solve. Since there are so many simplex iterations, I was hoping the DW algorithm would help due to its pricing approach.
Alternatively, should I try to go with Benders and fix the two binary variables (“ON” and “Switch”) instead?