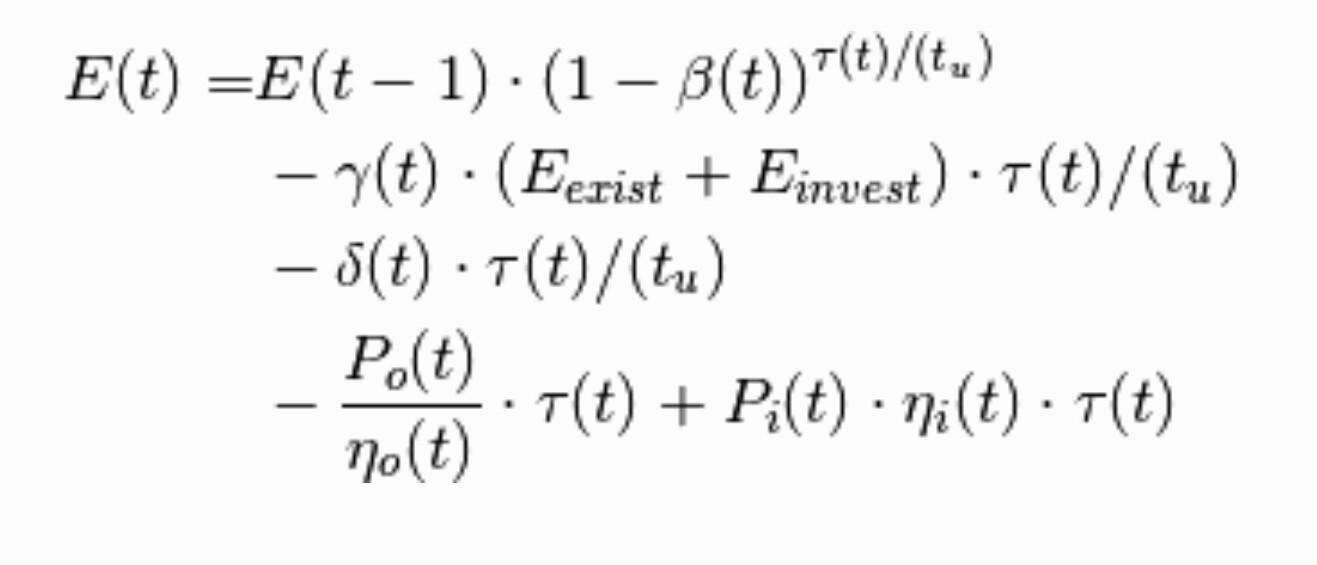GenericInvestmentStorageBlock model terms in Oemof

jess · 21 November 2021 08:48

Hello everybody,
This is the storage investment model in solph Oemof.

I’m wondering what is the meaning the of these terms in the model:

index of power $\tau(t)$ / $t_u$
$\gamma(t)$ * ( $E_{invest}$ + $E_{invest}$ ) * $\tau(t)$ / $t_u$
$\delta(t)$ * $\tau(t)$ / $t_u$
I’ve read the documentation but unfortunately I still not get the point. I’m familiar with input/ output conversion factors that consider the losses while charging and discharging, and the self discharge losses however I did not get the rest of losses $\gamma(t)$ and $\delta(t)$ considered in this model. By the way I have 1 hour as a time step in my model.

I would be very grateful if you could help me or maybe to recommend me a literature review where I could read more about this or an example from the reality where this losses are considered.

Thank you so much

pschoen · 22 November 2021 09:07

In my opinion, the documentation of the GenericStorageBlock (cf. oemof.solph package — oemof.solph 0.4.4 documentation) is a bit clearer.

t_u: time unit of losses and time increment, needed to make \tau dimensionless. When you give i.e. beta as losses per hour, |t_u| = 1, and you can just forget about it.
gamma term: Constant losses independent of the current content but dependent on the size of the storage. (I.e. due to minimum temperature in a thermal storage.)
delta term: Constant losses. (When you assume a heat storage to be of constant diameter, losses due to the minimum temperature that leave through the top/ bottom sides are independent from the size.)

I hope this helped.

jess · 22 November 2021 11:52

This definitely helps!
thanks so much!