Avoidance of circular flows caused by negative grid costs

Q&A
, , , , , , ,
6

Hi Brian,

I studied the non convexity due to battery storage losses (which includes the discussion of simultaneous charge and discharge) a few years ago:

(with author’s PDF version with a few bonuses available at Convex Storage Loss Modeling for Optimal Energy Management - Archive ouverte HAL)

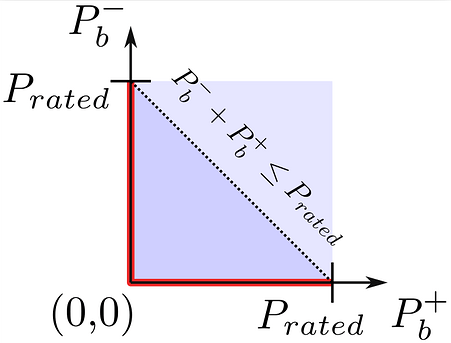
Forbidding the bidirectional flow in a battery is indeed a nonconvexity (see Fig 2 extracted from author’s version below: the red domain is nonconvex) that is typically modeled using a MILP (one binary variable for each time step):

Fig 2 from author's version "Complementarity constraint (bold red lines) + convex relaxation (dark blue triangle), vs box constraint (light blue square)"
Fig 2 from author's version "Complementarity constraint (bold red lines) + convex relaxation (dark blue triangle), vs box constraint (light blue square)"753×572 31.8 KB

Now, since my goal was to escape nonconvexity, I didn’t spend time on the MILP formulation, but it is in many of the references (including articles discussing to what extent it is legal to relax the binary constraints, but in the case of negative prices, as your experiments show, relaxation is wrong).

However, it is likely that indeed the MILP formulation depends on the rated power of the storage (P_{rated} on the figure). As a consequence, if the rated energy of the battery (which is proportional to P_{rated} is most models) isn’t a fixed parameter but rather an optimization variable, this probably creates a bilinearity (something like P_b^+ \leq P_{rated}.\delta with \delta \in {0,1}). However, it may be possible to replace the variable rated power by a fixed upper bound. I don’t know oemof internals so I don’t know I to implement this.

Now, in relation to @pschoen, I agree that including such binary constraints to forbid simultaneous charge and discharge can severely increase the solving time. However, I disagree with the idea that it is “a sign that something smells”. It’s just a situation of “downward flexibility shortage”. Also, I don’t think that including storage aging cost will solve the problem for sure (it may, but not for sure).

One quick and dirty way to circumvent the problem may be (if it doesn’t create a problem elsewhere in your study) to have zero storage losses (100% efficiency including any converter) so that the net effect of charge+discharge is zero. This would:

  1. cut the incentive to use circular flows for the optimization
  2. cancel the consequences of circular flows (no extraneous losses)